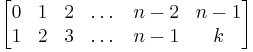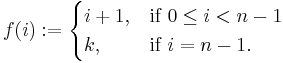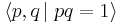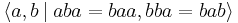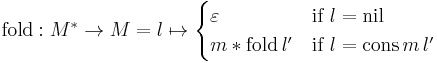Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for instance, they can be regarded as categories with a single object. Thus, they capture the idea of function composition within a set. Monoids are also commonly used in computer science, both in its foundational aspects and in practical programming. The transition monoid and syntactic monoid are used in describing finite state machines, whereas trace monoids and history monoids provide a foundation for process calculi and concurrent computing. Some of the more important results in the study of monoids are the Krohn-Rhodes theorem and the star height problem. The history of monoids, as well as a discussion of additional general properties, are found in the article on semigroups.
Contents |
Definition
A monoid is a set, S, together with a binary operation “•” (pronounced "dot" or "times") that satisfies the following three axioms:
- Closure
- For all a, b in S, the result of the operation a • b is also in S.
- Associativity
- For all a, b and c in S, the equation (a • b) • c = a • (b • c) holds.
- Identity element
- There exists an element e in S, such that for all elements a in S, the equation e • a = a • e = a holds.
And in mathematical notation we can write these as
- Closure:
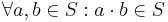 ,
, - Associativity:
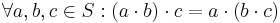 and
and - Identity element:
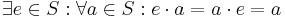 .
.
More compactly, a monoid is a semigroup with an identity element. It can also be thought of as a magma with associativity and identity. A monoid with invertibility property is a group.
The symbol for the binary operation is commonly omitted; for example the monoid axioms require  and
and 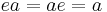 . This does not necessarily mean the variables are numbers being multiplied, any operation or elements may be used if they are well defined.
. This does not necessarily mean the variables are numbers being multiplied, any operation or elements may be used if they are well defined.
Monoid structures
Generators and submonoids
A submonoid of a monoid M is a subset N of M containing the unit element, and such that, if x,y ∈ N then x · y ∈ N. It is then clear that N is itself a monoid, under the binary operation induced by that of M. Equivalently, a submonoid is a subset N such that N=N*, where the superscript * is the Kleene star: the set is closed under composition or concatenation of its elements. For any subset N of M, the monoid N* is the smallest monoid that contains N.
A subset N is said to be a generator of M if and only if M=N*. If there is a finite generator of M, then M is said to be finitely generated.
Commutative monoid
A monoid whose operation is commutative is called a commutative monoid (or, less commonly, an abelian monoid). Commutative monoids are often written additively. Any commutative monoid is endowed with its algebraic preordering ≤, defined by x ≤ y if and only if there exists z such that x + z = y. An order-unit of a commutative monoid M is an element u of M such that for any element x of M, there exists a positive integer n such that x ≤ nu. This is often used in case M is the positive cone of a partially ordered abelian group G, in which case we say that u is an order-unit of G.
Partially commutative monoid
A monoid for which the operation is commutative for some, but not all elements is a trace monoid; trace monoids commonly occur in the theory of concurrent computation.
Examples
- Every singleton set {x} gives rise to a particular one-element (trivial) monoid. The monoid axioms require that x*x = x in this case.
- Every group is a monoid and every abelian group a commutative monoid.
- Every bounded semilattice is an idempotent commutative monoid.
- In particular, any bounded lattice can be endowed with both a meet- and a join- monoid structure. The identity elements are the lattice's top and its bottom, respectively. Being lattices, Heyting and Boolean algebra are endowed with these monoid structures.
- Any semigroup S may be turned into a monoid simply by adjoining an element e not in S and defining e*s = s = s*e for all s ∈ S. This conversion of any semigroup to the monoid is done by the free functor between the category of semigroups and the category of monoids .
- Thus, an idempotent monoid (sometimes known as find-first) may be formed by adjoining an identity element e to the left zero semigroup over a set S. The opposite monoid (sometimes called find-last) is formed from the right zero semigroup over S.
- Adjoin an identity e to the left-zero semigroup with two elements {lt; gt}. Then the resulting idempotent monoid {lt; e; gt} models the lexicographical order of a sequence given the orders of its elements, with e representing equality.
- Thus, an idempotent monoid (sometimes known as find-first) may be formed by adjoining an identity element e to the left zero semigroup over a set S. The opposite monoid (sometimes called find-last) is formed from the right zero semigroup over S.
- The natural numbers, N, form a commutative monoid under addition (identity element zero), or multiplication (identity element one). A submonoid of N under addition is called a numerical monoid.
- The positive integers, N-{0}, form a commutative monoid under multiplication (identity element one).
- The elements of any unital ring, with addition or multiplication as the operation.
- The integers, rational numbers, real numbers or complex numbers, with addition or multiplication as operation.[1]
- The set of all n by n matrices over a given ring, with matrix addition or matrix multiplication as the operation.
- The set of all finite strings over some fixed alphabet Σ forms a monoid with string concatenation as the operation. The empty string serves as the identity element. This monoid is denoted Σ∗ and is called the free monoid over Σ.
- Given any monoid M, the opposite monoid Mop has the same carrier set and identity element as M, and its operation is defined by x *op y = y * x. Any commutative monoid is the opposite monoid of itself.
- Given two sets M and N endowed with monoid structure (or, in general, any finite number of monoids, M1, ..., Mk), their cartesian product M × N is also a monoid (respectivelly, M1 × ... × Mk). The associative operation and the identity element are defined pairwise.[2]
- Fix a monoid M. The set of all functions from a given set to M is also a monoid. The identity element is a constant function mapping any value to the identity of M; the associative operation is defined pointwise.
- Fix a monoid M with the operation * and identity element e, and consider its power set P(M) consisting of all subsets of M. A binary operation for such subsets can be defined by S * T = {s * t : s in S and t in T}. This turns P(M) into a monoid with identity element {e}. In the same way the power set of a group G is a monoid under the product of group subsets.
- Let S be a set. The set of all functions S → S forms a monoid under function composition. The identity is just the identity function. It is also called the full transformation monoid of S. If S is finite with n elements, the monoid of functions on S is finite with nn elements.
- Generalizing the previous example, let C be a category and X an object in C. The set of all endomorphisms of X, denoted EndC(X), forms a monoid under composition of morphisms. For more on the relationship between category theory and monoids see below.
- The set of homeomorphism classes of compact surfaces with the connected sum. Its unit element is the class of the ordinary 2-sphere. Furthermore, if a denotes the class of the torus, and b denotes the class of the projective plane, then every element c of the monoid has a unique expression the form c=na+mb where n is the integer ≥ 0 and m=0,1, or 2. We have 3b=a+b.
- Let
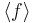 be a cyclic monoid of order n, that is,
be a cyclic monoid of order n, that is, 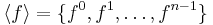 . Then
. Then 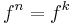 for some
for some 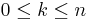 . In fact, each such k gives a distinct monoid of order n, and every cyclic monoid is isomorphic to one of these.
. In fact, each such k gives a distinct monoid of order n, and every cyclic monoid is isomorphic to one of these.
Moreover, f can be considered as a function on the points  given by
given by
or, equivalently
Multiplication of elements in 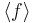 is then given by function composition.
is then given by function composition.
Note also that when 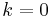 then the function f is a permutation of
then the function f is a permutation of  and gives the unique cyclic group of order n.
and gives the unique cyclic group of order n.
Properties
In a monoid, one can define positive integer powers of an element x : x1=x, and xn=x*...*x (n times) for n>1 . The rule of powers xn+p=xn * xp is obvious.
Directly from the definition, one can show that the identity element e is unique. Then, for any x , one can set x0=e and the rule of powers is still true with nonnegative exponents.
It is possible to define invertible elements: an element x is called invertible if there exists an element y such that x*y = e and y*x = e. The element y is called the inverse of x . If y and z are inverses of x, then by associativity y = (zx)y = z(xy) = z. Thus inverses, if they exist, are unique.[3]
If y is the inverse of x , one can define negative powers of x by setting x−1=y and x−n=y*...*y (n times) for n>1 . And the rule of exponents is still verified for all n,p rational integers. This is why the inverse of x is usually written x−1. The set of all invertible elements in a monoid M, together with the operation *, forms a group. In that sense, every monoid contains a group (if only the trivial one consisting of the identity alone).
However, not every monoid sits inside a group. For instance, it is perfectly possible to have a monoid in which two elements a and b exist such that a*b = a holds even though b is not the identity element. Such a monoid cannot be embedded in a group, because in the group we could multiply both sides with the inverse of a and would get that b = e, which isn't true. A monoid (M,*) has the cancellation property (or is cancellative) if for all a, b and c in M, a*b = a*c always implies b = c and b*a = c*a always implies b = c. A commutative monoid with the cancellation property can always be embedded in a group via the Grothendieck construction. That's how the additive group of the integers (a group with operation +) is constructed from the additive monoid of natural numbers (a commutative monoid with operation + and cancellation property). However, a non-commutative cancellative monoid need not be embeddable in a group.
If a monoid has the cancellation property and is finite, then it is in fact a group. Proof: Fix an element x in the monoid. Since the monoid is finite, xn = xm for some m > n > 0. But then, by cancellation we have that xm-n = e where e is the identity. Therefore x * xm-n-1 = e, so x has an inverse.
The right- and left-cancellative elements of a monoid each in turn form a submonoid (i.e. obviously include the identity and not so obviously are closed under the operation). This means that the cancellative elements of any commutative monoid can be extended to a group.
An inverse monoid is a monoid where for every a in M, there exists a unique a-1 in M such that a=a*a-1*a and a-1=a-1*a*a−1. If an inverse monoid is cancellative, then it is a group.
Acts and operator monoids
Let M be a monoid, with the binary operation denoted by “•” and the identity element denoted by e. Then a (left) M-act (or left act over M) is a set X together with an operation ⋅ : M × X → X which is compatible with the monoid structure as follows:
- for all x in X: e ⋅ x = x;
- for all a, b in M and x in X: a ⋅ (b ⋅ x) = (a • b) ⋅ x.
This is the analogue in monoid theory of a (left) group action. Right M-acts are defined in a similar way. A monoid with an act is also known as an operator monoid. Important examples include transition systems of semiautomata. A transformation semigroup can be made into an operator monoid by adjoining the identity transformation.
Monoid homomorphisms
A homomorphism between two monoids (M,*) and (M′,•) is a function f : M → M′ such that
- f(x*y) = f(x)•f(y) for all x, y in M
- f(e) = e′
where e and e′ are the identities on M and M′ respectively. Monoid homomorphisms are sometimes simply called monoid morphisms.
Not every semigroup homomorphism is a monoid homomorphism since it may not preserve the identity. Contrast this with the case of group homomorphisms: the axioms of group theory ensure that every semigroup homomorphism between groups preserves the identity. For monoids this isn't always true and it is necessary to state it as a separate requirement.
A bijective monoid homomorphism is called a monoid isomorphism. Two monoids are said to be isomorphic if there is an isomorphism between them.
Equational presentation
Monoids may be given a presentation, much in the same way that groups can be specified by means of a group presentation. One does this by specifying a set of generators Σ, and a set of relations on the free monoid Σ∗. One does this by extending (finite) binary relations on Σ∗ to monoid congruences, and then constructing the quotient monoid, as above.
Given a binary relation R ⊂ Σ∗ × Σ∗, one defines its symmetric closure as R ∪ R−1. This can be extended to a symmetric relation E ⊂ Σ∗ × Σ∗ by defining x ~E y if and only if x = sut and y = svt for some strings u, v, s, t ∈ Σ∗ with (u,v) ∈ R ∪ R−1. Finally, one takes the reflexive and transitive closure of E, which is then a monoid congruence.
In the typical situation, the relation R is simply given as a set of equations, so that 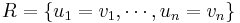 . Thus, for example,
. Thus, for example,
is the equational presentation for the bicyclic monoid, and
is the plactic monoid of degree 2 (it has infinite order). Elements of this plactic monoid may be written as 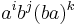 for integers i, j, k, as the relations show that ba commutes with both a and b.
for integers i, j, k, as the relations show that ba commutes with both a and b.
Relation to category theory
| Group-like structures | ||||
| Totality | Associativity | Identity | Inverses | |
|---|---|---|---|---|
| Group | Yes | Yes | Yes | Yes |
| Monoid | Yes | Yes | Yes | No |
| Semigroup | Yes | Yes | No | No |
| Loop | Yes | No | Yes | Yes |
| Quasigroup | Yes | No | No | No |
| Magma | Yes | No | No | No |
| Groupoid | No | Yes | Yes | Yes |
| Category | No | Yes | Yes | No |
| Semicategory | No | Yes | No | No |
Monoids can be viewed as a special class of categories. Indeed, the axioms required of a monoid operation are exactly those required of morphism composition when restricted to the set of all morphisms whose source and target is a given object. That is,
- A monoid is, essentially, the same thing as a category with a single object.
More precisely, given a monoid (M,*), one can construct a small category with only one object and whose morphisms are the elements of M. The composition of morphisms is given by the monoid operation *.
Likewise, monoid homomorphisms are just functors between single object categories. So this construction gives an equivalence between the category of (small) monoids Mon and a full subcategory of the category of (small) categories Cat. Similarly, the category of groups is equivalent to another full subcategory of Cat.
In this sense, category theory can be thought of as an extension of the concept of a monoid. Many definitions and theorems about monoids can be generalised to small categories with more than one object. For example, a quotient of a category with one object is just a quotient monoid.
Monoids, just like other algebraic structures, also form their own category, Mon, whose objects are monoids and whose morphisms are monoid homomorphisms.
There is also a notion of monoid object which is an abstract definition of what is a monoid in a category. A monoid object in Set is just a monoid.
Monoids in computer science
In computer science, many abstract data types can be endowed with a monoid structure. In a common pattern, a sequence of elements of a monoid is "folded" or "accumulated" to produce a final value. For instance, many iterative algorithms need to update some kind of "running total" at each iteration; this pattern may be elegantly expressed by a monoid operation. Alternatively, the associativity of monoid operations ensures that the operation can be parallelized by employing a prefix sum or similar algorithm, in order to utilize multiple cores or processors efficiently.
Given a sequence of values of type M with identity element 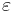 and associative operation
and associative operation  , the fold operation is defined as follows:
, the fold operation is defined as follows:
In addition, any data structure can be 'folded' in a similar way, given a serialization of its elements. For instance, the result of "folding" a binary tree might differ depending on pre-order vs. post-order tree traversal.
See also
References
- John M. Howie, Fundamentals of Semigroup Theory (1995), Clarendon Press, Oxford ISBN 0-19-851194-9
- Jacobson, Nathan (1951), Lectures in Abstract Algebra, I, D. Van Nostrand Company, ISBN 0-387-90122-1
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
- M. Kilp, U. Knauer, A.V. Mikhalev, Monoids, Acts and Categories with Applications to Wreath Products and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter, 2000, ISBN 3110152487.
- Weisstein, Eric W., "Monoid" from MathWorld.
- Monoid at PlanetMath.